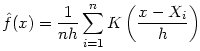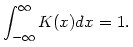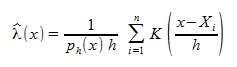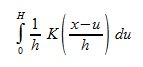| Designed by: |
| Densità di Popolazione con QGis |
 |
 |
 |
| Interessi - Informatica |
|
Obiettivo dell'articolo è di introdurre il lettore ad un metodo per costruire una mappa di densità della popolazione residente in un centro urbano per mezzo di strumenti GIS open source, in particolare Quantum GIS 1.7.0.
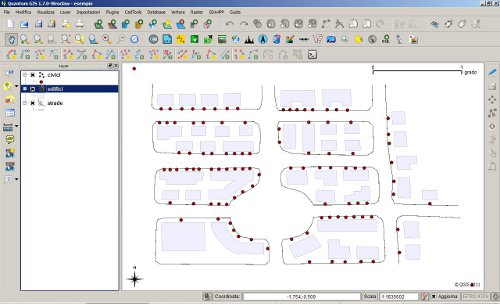
La residenza di una persona viene individuata, generalmente, attraverso un indirizzo, ovvero una tripla di valori: area di circolazione, civico, interno. Ad es. (Via Garibaldi, 5, 3). Per semplicità si ometterà di dettagliare i casi in cui intervengono il "barrato" che si assumerà come parte del civico, la "scala" ed il "piano" che si assumeranno parti dell'interno. Dal punto di vista materiale il numero civico è una targa che deve essere apposta in corrispondenza dell'accesso di una proprietà privata al suolo pubblico (una porta, un cancello, ecc...), mentre l'interno è generalmente una targa apposta presso l'ingresso ad un'unità immobiliare. La georeferenziazione corretta di un numero civico in un GIS viene effettuata disegnando un'entità di geometria puntiforme in corrispondenza dell'accesso al suolo pubblico. Nel seguito, per semplificare ulteriormente la trattazione, si prenderà in esame il caso in cui tutti gli indirizzi di residenza del campione in esame siano sprovvisti di interno, considerando pertanto la sola copertura puntiforme dei numeri civici ed evitando di trattare la costruzione della copertura degli interni. Le aree di circolazione vengono generalmente codificate in uno stradario che, per ogni area, riporta almeno un codice ed una descrizione. La tabella degli attributi della copertura dei numeri civici, tipicamente, comprenderà il codice del numero civico, il codice dell'area di circolazione, il numero civico. La residenza di una persona può quindi venire georeferenziata tramite associazione al punto numero civico. Solitamente, in una banca dati anagrafica l'associazione non è diretta ma mediata dall'appartenenza ad una famiglia, cioè: una persona appartiene ad un nucleo famigliare il quale è associato ad un numero civico. Per costruire la mappa di densità, si procede a costruire un progetto d'esempio, che contiene tre coperture: una lineare che rappresenta i bordi strada, una poligonale a rappresentare gli edifici, la copertura puntuale dei numeri civici costuita come descritto sopra. In Figura 1 viene mostrato il progetto "esempio.qgs" caricato in Quantum GIS con le tre coperture vettoriali: alcune strade, 40 edifici ed un centinaio di civici, in modo tale da simulare la vettorializzazione di qualche isolato di un centro urbano.
Figura 1
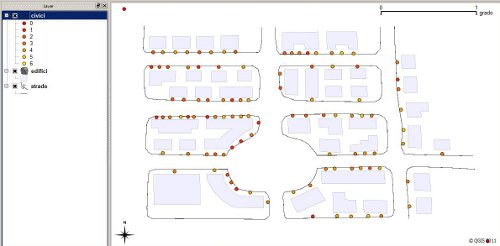
Il secondo passo consiste nell'associare ad ogni numero civico il numero di persone ivi residente. L'operazione può essere fatta agevolmente tramite un conteggio sulle tabelle d'anagrafe e riportando il dato, per ogni civico, sulla tabella degli attributi. Nella pratica, si modifica la tabella degli attributi della copertura dei civici aggiungendo un campo ("numero_abitanti") e compilandolo con i risultati del conteggio. Ad ogni civico sarà quindi associato il numero di residenti che vi afferiscono. Possiamo verificare graficamente il risultato dell'operazione, assegnando allo stile della copertura un simbolo graduato tramite una scala di colori. Nella copertura d'esempio sono presenti civici ai quali afferiscono da 0 a 6 persone, pertanto basterà la definizione di una scala su 7 classi, dal rosso al giallo.
Figura 2
Dalla figura si può notare che nonostante venga già evidenziata graficemente, tramite i colori, la configurazione della popolazione sul territorio, la mappa è poco leggibile, non è possibile infatti ottenere una visione precisa della distribuzione della densità di popolazione. Per costruire la mappa di densità si dovranno utilizzare opportuni strumenti, che fanno riferimento al concetto di smoothing dei dati. In particolare si tratteranno i civici come processo puntule bidimensionale e si utilizzerà il modello di stima dell'intensità locale dei punti proposto da Diggle [1985]. La funzione di stima di densità di probabilità Kernel, con Kernel K, è definita dalla formula:
dove h viene detto parametro di smoothing o larghezza di banda, e con K che soddisfa la proprietà:
Supponendo la presenza di n punti nell'intervallo (0, H) la funzione di stima d'intensità è definita dalla formula:
con la funzione di correzione p definita da:
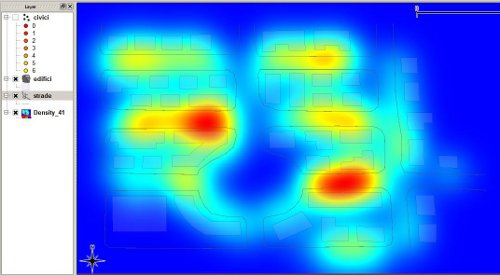
In QGis, nel Plugin SDA4PP è presente il tool Kernel Smoothed Intensity of Point Pattern che utilizza gli strumenti di analisi spaziale presenti in R, ed in particolare la funzione density che implementa la funzione di stima d'intensità descritto sopra. Come funzione K viene utilizzato il kernel Gaussiano isotropico con i punti di massa localizzati nei punti della copertura indicata nel tool. Se viene valorizzato il parametro weigths i punti di massa acquistano il peso indicato. Il risultato è una convoluzione del kernel Gaussiano calcolata utilizzando la trasformata di Fourier. Applicando il tool alla copertura dei civici, indicando il campo "numero_abitanti" come peso, e scegliendo un opportuno valore di larghezza di banda e di rifinitura della griglia, costruiamo una mappa di densità raster (tramite le librerie GDAL) della popolazione residente. In figura 3 il risultato.
Figura 3
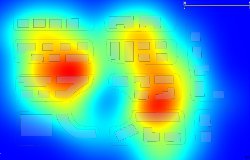
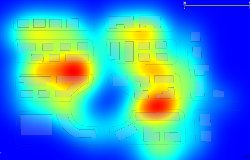
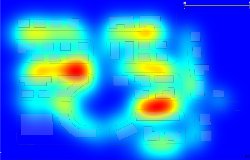
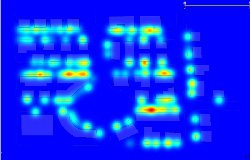
Questione chiave per la bontà del risultato è la scelta del parametro di smoothing. La qualità della stima, e della mappa in output dipende pesantemente da questa scelta e solo in seconda istanza dalla scelta della funzione Kernel. La decisione dovrà tenere conto della scala alla quale sarà visualizzata la mappa e degli usi che se ne dovranno fare, in modo tale da orientarsi ad una visione d'insieme o di maggior dettaglio relativamente alla porzione di territorio oggetto di studio. Le figure che seguono mostrano come varia il risultato in funzione della scelta del paramentro.
h = 0.304 h = 0.250
h = 0.200 h = 0.150
h = 0.100 h = 0.050
Rosenblatt, M. (1956) - Remarks on some non-parametric estimates of a density function. Ann. Math. Statist., 27, 832-7. Diggle, P. (1985) - A Kernel Method for Smoothing Point Process Data. Journal of the Royal Statistical Society. Series C (Applied Statistics), Vol. 34, No. 2, pp. 138-147 |